二阶电路时域分析的数学基础
引言:电容的电流是其电压对时间的一阶导数,电感的电流是其电压在时间上的积分。对于含有电容和电感的电路列方程,方程中会同时含有导数及积分的项。为了消去积分项,我们需要在方程两端都对时间求导,这样方程中原来的一阶导数就会变成二阶导数。因此,对于此类问题,我们需要用二阶微分方程来描述。其解的形式与一阶微分方程会有很大的不同,值得我们专门去研究。由一个电容、一个电感、一个电阻的串联电路(RLC串联电路),就可以用二阶线性常系数微分方程去描述,本文以求解该方程为例,顺便整理二阶微分方程所需要的数学知识。由于二阶微分方程的解十分复杂,因此本文会在计算过程中加入许多约束条件,并仅会研究在这些约束条件下二阶微分方程的解。对本文的任何疑问,都可以联系作者(联系方式见:www.diqiuyi.org “关于”页面)。
索引(可以尝试单击下面的标题):
正文:
一 求解齐次微分方程(零输入响应)
需要求解的方程:
注释:其中v(t)是我们要求解的函数,t是自变量,R、L、C均是数值为正的实常数。这是一个二阶常系数齐次线性微分方程。
我们要解这个微分方程,需要知道该方程解的结构。下面以定理的形式给出:
1.1 寻找两个线性无关的解
我们要找到这个通解,就要先找到两个线性无关的解。因为指数函数微分形式不变,所以尝试以指数函数作为方程的解。
1.1.1 设出解的形式
注释:
1、我们没必要设解为:
因为我们只想找到一个解,不妨设A=1,从而简化问题。而且不同的A对应的解是线性相关的。
2、其中s是常数(注意:s是复数也可以,因为即使它是复数,指数函数微分形式还是不变的,仍然可能是方程的解)。
1.1.2 把解代回原方程
把解代入原方程,我们得到:
注释:该方程称作微分方程的特征方程,该方程也可通过观察原微分方程直接得出。
1.1.3 求出这个解
应用求根公式,得:
在此,我们先定义一些常数:
(1)、衰减因子,衰减常数,damping factor
该常数随不同电路结构而发生改变,在该RLC串联电路中:
(2)、无阻尼自然频率,简谐振荡频率,undamped natural frequency,simply resonance frequency
(3)、阻尼自然频率,damped natural frequency
(4)、品质因数,quality factor
注释:这些定义只不过是,把关于原方程中常数RLC的一些算式,用其它字母替代了而已。这在数学上没有什么道理可言。我们做此定义完全是基于实际物理意义的考虑,在此处暂不做深入讨论。
用以上定义的常数表示s,得:
1.2 求齐次微分方程的通解
对与原方程中常数的不同取值,s1、s2可能是两个不相等的实数、两个相等的实数或两个共轭复数,本文中仅研究第三种情况。其约束条件如下:
欠阻尼条件:
注释:在RLC串联电路中,该条件等价于:
因此,微分方程两个线性无关的解为:
由二阶齐次线性微分方程解的结构可知:
也是微分方程的两个线性无关的解。
因此,微分方程的通解可写成:
注释:该通解仅在欠阻尼条件下成立,否则通解将会是完全不同的形式!
1.3 求齐次微分方程的唯一解
在确定通解中任意常数之前,先准备一些要用到的等式:
对v(t)进行三角恒等变换,得:
对v(t)求导,得:
1.3.1 由初始条件确定方程的唯一解
已知初始条件:
把初始条件代入通解,得:
因此,求得在该初始条件下的v(t):
注释:该解仅在欠阻尼条件下成立,否则解将会是完全不同的形式!
1.3.2 解在约束条件下的化简
我们最终解出的函数比较复杂,为了看清它的性质,我们引入约束条件,对此进行化简:
电感初始电流为零:
在该约束条件下化简为:
仍然比较复杂,我们再引入另外一个约束条件:
深度欠阻尼条件:
注释:
1、在RLC串联电路中,该条件等价于:
显然,如果满足了深度欠阻尼条件,则欠阻尼条件也一定会同时满足。
2、在此列出一些等价的条件,这些条件在后文中会被依次使用到。
3、深度欠阻尼是为了方便说明作者自拟的词汇,并无此专业词汇。
在此条件下,微分方程的解最终可以化简为:
二 求解非齐次微分方程
另外一个需要求解的方程:
我们要求解它,需要先知道其解的结构,下面以定理的形式给出:
2.1 求非齐次微分方程的通解
2.1.1 观察法求特解
注释:由二阶线性微分方程解的结构得知,原方程的解有无穷多个,但我们只要随便找到其中一个(这个解就叫特解),就可以据此写出通解,这就是我们在此处能够应用观察法的原因。在该例中,由于存在着与自变量t无关的常数解,因此比较容易用观察法得到。当然,有的微分方程的特解形式十分复杂,根本不可能用观察法得出,本文对此不做深入讨论。
2.1.2 类比求齐次解
该方程对应的齐次方程恰好就是我们之前讨论过的那个齐次方程,因此它的通解为:
注释:这个解仅在欠阻尼条件下才成立。
2.1.3 写出全解
注释:这个解仅在欠阻尼条件下才成立。
2.2 求非齐次微分方程的唯一解
在此之前,先准备一些要用到的等式:
2.2.1 由零初始条件确定的唯一解(零状态响应)
如果初始条件为:
代入通解,得:
写出该初始条件下的解:
在深度欠阻尼约束条件下:
2.2.2 由非零初始条件确定的唯一解(全响应)
如果初始条件为:
代入初始条件,得:
写出该初始条件下的解:
从这里我们可以明显的看出,全响应是零输入响应和零状态响应的线性叠加。
在电感初始电流为零,和深度欠阻尼双重约束条件下,该解可以化简为:
三 附录
从草稿中删除的内容,及写作过程中顺便研究的一些杂七杂八的内容,整理在此。忽略本附录不会影响阅读本文。
3.1 辅助角公式:
这在本文公式推导里面用过,对于它的成立条件一般书上并没有明确给出,这里稍微提一下:
3.2 微分与导数的区别
纯粹好奇而翻书,在此摘录一点:
对于一元函数来说,函数的微分等于函数的导数与自变量微分的乘积。
3.3 品质因数Q的物理意义
从我们最后我们得到的方程来看
过了Q个周期,指数项衰减为:
因为在该方程中,指数函数相当于余弦函数的振幅,如果我们认为振幅衰减到初始的4%就算停止振荡,那么Q的物理意义就是振荡的周期数。
注释:
1、这个结论是我们在电感初始电流为零,和深度欠阻尼双重约束条件下得出的,深度欠阻尼的一种等价描述是:
2、指数项衰减程度与经过的周期数之间关系
|
衰减到原先的的多少 |
经过多少Q个振荡周期 |
|
4% |
一个 |
|
20% |
半个 |
|
50% |
0.22个 |
|
73% |
十分之一个 |
地球仪(www.diqiuyi.org)
2012年9月14日
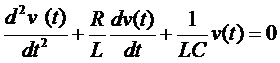
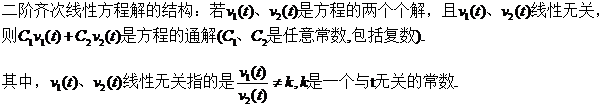
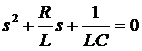
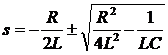
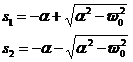
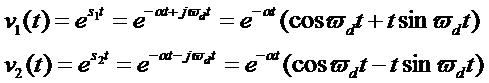
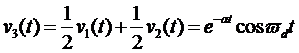
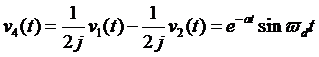
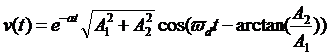
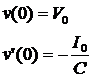
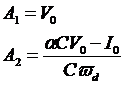
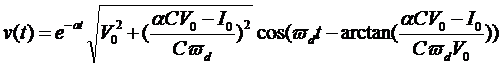
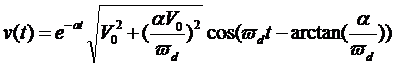
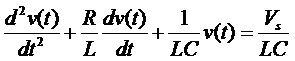
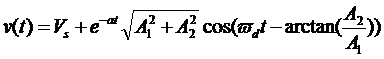
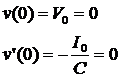
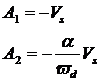
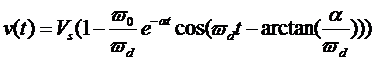
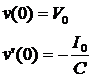
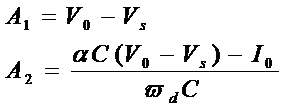
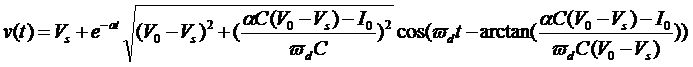
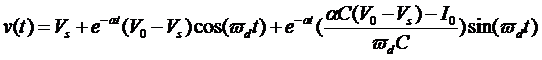
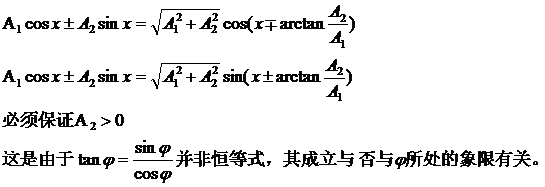
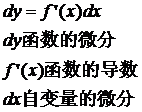
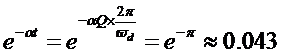
这个我也要好好学习学习